TP8 : arts graphiques

info@mp2i-pv

TP8 : arts graphiques

Ce TP est à faire avec un éditeur de texte, en compilant et exécutant en ligne de commande, avec les options -Wall, -Wpedantic et -Wconversion du compilateur gcc. Si vous n’avez pas de machine avec ce qu’il faut, vous pouvez vous connecter sur le site jupyter de TP, et dans le menu déroulant “New” choisir “Terminal” pour avoir un terminal ou “Text File” pour ouvrir une fenêtre dans un éditeur de texte (cet éditeur propose indentation automatique et coloration syntaxique en choisissant le langage “C” dans le menu déroulant “Language”, et vous pouvez demander un comportement à la emacs en sélectionnant “emacs” dans le menu déroulant “Edit”). Dans ce cas, créez un répertoire TP8 et mettez tout votre code dedans.

Ce TP est à faire sur 3 semaines, nous commençons en TP, mais c’est ensuite à vous de continuer, ce qui vous permettra de continuer à faire du C pendant que nous commencerons ocaml ensemble. Le rendu se fait soit sur le site de TP, dans un répertoire TP8, soit dans un dépôt github si vous préférez (dépôt privé où vous m’aurez ajoutée, mon identifiant github étant inesKKK).

Dans ce TP, on se propose de représenter en 2D une scène (simple) en 3D. La scène est constituée d’un ensemble de rectangles dont les côtés sont parallèles aux axes, chaque rectangle ayant sa propre profondeur et sa propre couleur, tous les rectangles étant alignés selon le même axe. L’observateur est dans un premier temps supposé à une profondeur plus petite que celle de tous les rectangles et tourné dans le sens des profondeurs croissantes, selon le même axe que les rectangles.

Par exemple dans la situation suivante:

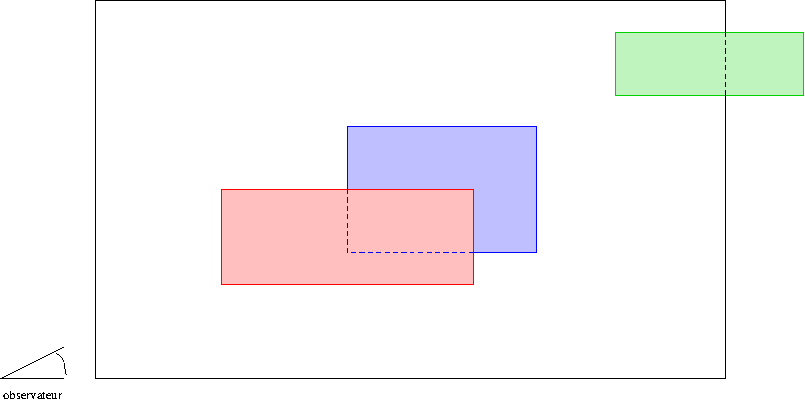
on veut obtenir le tableau

Partie du code fournie

On vous fournit deux fichiers d’en-tête:

et un fichier de code couleur.c que vous ne devez pas modifier et qui contient la définition de la couleur blanc et de la fonction d’affichage de la couleur.

Votre rôle est de compléter le fichier peintre.c qui pour l’instant contient la fonction main et une fonction correspondant à l’exemple de l’énoncé. Toutes les fonctions à écrire sont déclarées dans le fichier peintre.h

Pour l’instant, les fonctions n’étant pas définies, ça ne compile pas, mais à terme pour compiler il faudra utiliser la ligne de commande gcc couleur.c peintre.c.

Tests

C’est à vous d’écrire des fonctions de test. Pour toute fonction, les tests seront inclus dans une fonction appelée tests_fonction où fonction est remplacé par le nom de la fonction. Par exemple tests_canevas pour tester la fonction canevas. Ces fonctions seront construites en suivant le plan : construction des entrées, tests avec assert que les sorties correspondantes sont correctes. (N’oubliez pas d’inclure assert.h.)

Fond de toile - semaine 1

Comme tout peintre, vous avez besoin d’une toile pour vous exprimer, nous allons donc commencer par là.

Exercice 1 :

Écrire la fonction canevas qui permet d’obtenir une toile complètement blanche.

Exercice 2 :

Écrire la fonction detruit_toile qui permet de libérer toute la mémoire allouée par canevas. Vous pouvez tester votre programme en lançant valgrind avec comme argument le nom de votre exécutable (en appelant successivement dans le main les focntions canevas et detruit_toile).

Rectangle par rectangle

Dans un premier temps, mettons en place des fonctions qui permettent de dessiner un rectangle sur une toile existante (blanche ou non).

Exercice 3 :

Écrire une fonction trace qui permet de modifier la couleur des pixels d’un tableau dans les limites du rectangle fourni en argument, en mettant ces pixels à la couleur du rectangle.

Exercice 4 :

Pour voir votre tableau, nous allons utiliser une format d’image appelé PPM P3. C’est un format très simple qui s’écrit en ASCII. Il contient essentiellement:

(regardez l’exemple sur wikipedia si vous ne comprenez pas)

Écrire une fonction affiche qui prend en argument un tableau et écrit sur la sortie standard le fichier PPM qui lui est associé (le fichier couleur.c contient une fonction qui permet d’écrire les entiers correspondants à une couleur).

Exercice 5 :

Le main fourni permet d’afficher l’exemple de l’énoncé. Exécuter le programme en redirigeant la sortie sur le fichier enonce.ppm et regarder le résultat grâce à la commande display enonce.ppm.

Recommencer en affichant la production de la fonction suprematism1915 et vérifier que le résultat ressemble à ça:

Famille de rectangles - semaine 2

Maintenant que vous savez peindre, attaquons-nous à des scènes plus réalistes (bon toujours à base de rectangles, ce qui limite quand même).

Dans une scène plus réaliste, on ajoute aux rectangles une information concernant leur profondeur, et bien sûr l’observateur ne peut pas voir à travers les objets (qui sont tous opaques par hypothèse). Quand deux rectangles se superposent, c’est donc la couleur du rectangle le plus proche de l’observateur qui est affichée.

À cette fin, nous allons ranger les rectangles dans une liste chaînée, du plus éloigné au plus proche, ce qui permettra de tracer les rectangles en parcourant la liste sans se poser de question (au pire et de façon momentanée, certains pixels n’auront pas la bonne couleur, mais tout finira par rentrer dans l’ordre).

Dans cette partie, vous devez écrire vous-mêmes le fichier d’en-tête liste.h et compléter le fichier peintre.c.

Exercice 6 :

Déclarer dans le fichier liste.h un type struct maillon qui est le maillon d’une liste simplement chaînée et qui contient:

Dans la suite, une liste de rectangles désigne l’adresse d’un tel maillon. Une liste vide est donc le pointeur NULL.

Déclarer dans liste.h et définir dans peintre.c une fonction perspective qui prend en argument l’adresse d’une toile et une liste de rectangles supposée correctement triée (du rectangle le plus éloigné au rectangle le plus proche) et modifie la toile transmise pour y dessiner la vue correspondant à la scène décrite par la liste.

Exercice 7 :

Écrire une fonction ajout_objet qui prend en argument une liste de rectangles, un rectangle et une profondeur, ajoute ce rectangle dans la liste au bon endroit, et renvoie la tête de liste de la nouvelle liste.

Exercice 8 :

Reconstituer en passant par une liste de rectangles la peinture Composition en rouge, jaune, bleu et noir de Mondrian :

(je ne veux entendre personne me dire que ce n’est pas plus réaliste que la peinture de Malevitch), ou créer une scène à la Minecraft de ce genre:

Promenade autour de la scène - semaine 3

L’observateur peut maintenant se déplacer dans l’axe perpendiculaire à la scène, et se retourner à 180°, si bien qu’il peut voir une partie seulement des objets, et dans un sens ou dans l’autre. Ajouter ce qu’il faut pour que ce soit possible, et proposer plusieurs visions de la même scène.