TP17 : Parcours d’arbres

Arbres binaires

Cette partie est à faire en C.

Le but de cette partie est d’afficher des arbres binaires de plusieurs façons.

Les types à utiliser et les en-têtes des fonctions à implémenter sont disponibles dans le fichier arbres.h.

Les exemples de l’énoncé seront donnés sur l’arbre renvoyé par la fonction exemple disponible dans les fichiers exemple.h / exemple.c.

Parcours en largeur

Pour un parcours en largeur, il faut utiliser des files, je vous fournis une implémentation: files.h / files.c

Exercice 1 : parcours simple

Écrire une fonction parcours_largeur qui affiche par niveau, en laissant un espace entre les étiquettes. L’exemple fourni doit donner l’affichage suivant:

$ ./a.out 
a b c d e f g h i j 

Exercice 2 : parcours par niveau

On veut maintenant afficher le contenu de l’arbre par niveau, comme suit:

$ ./a.out
a 
b c 
d e f 
g h i 
j 

Pour cela, vous allez insérer dans la file un pointeur nul à la fin de chaque niveau qui n’est pas le dernier niveau. L’extraction d’un tel pointeur de la file vous permettra de savoir que vous avez fini d’afficher un niveau.

Exercice 3 [difficile] : joli affichage d’un arbre parfait

Pour cet exercice, vous trouverez la fonction exemple_parfait dans le fichier exemple.c qui vous permet de récupérer un arbre parfait en spécifiant sa hauteur.

On veut maintenant afficher le contenu d’arbre parfait par niveau, en décalant, comme suit:

       a        
   b       c    
 d   e   f   g  
h i j k l m n o 

Pour cela, vous aller vous servir de l’attribut espace du type struct arbre. Pour chaque feuille d’un arbre parfait, cet attribut doit valoir 0. Pour chaque nœud interne d’un arbre parfait, il doit valoir $2e+1$ ou $e$ est la valeur de l’attribut pour un fils de ce nœud.

1. Écrire une fonction

   int remplir_espaces(struct arbre *a, int h);
   

   qui permet de donner les valeurs aux attributs espace de l’arbre a de hauteur h.

2. Écrire une fonction

   void joli_affichage_arbre_parfait(struct arbre *a)
   

   qui fait l’affichage comme ci-dessus. L’étiquette d’un nœud doit être précédée et suivie du nombre d’espaces spécifié dans l’attribut espace de ce nœud. Il faut par ailleurs ajouter un espace entre deux étiquettes voisines sur un niveau.

Parcours préfixe

On va maintenant afficher un arbre à la manière de pstree (essayez dans un terminal pour voir).

Exercice 4 : parcours simple

Écrire une fonction parcours_prefixe qui prend en argument un pointeur sur arbre et affiche son parcours préfixe avec retour à la ligne entre chaque étiquette. Sur l’exemple de l’énoncé, on obtient:

$ ./a.out 
a
b
d
e
g
j
c
f
h
i

Exercice 5 [difficile] : décalages

Écrire une fonction parcours_decale qui prend en argument un pointeur sur arbre et permet un affichage décalé. Sur l’exemple de l’énoncé, on doit obtenir:

a
--b
----d
----e
------g
--------j
--c
----f
------h
------i

Exercice 6 [challenge] : sans retours à la ligne inutiles

Écrire une fonction joli_parcours_decale qui prend en argument un pointeur sur arbre et permet un affichage décalé sans retours à la ligne inutiles. Sur l’exemple de l’énoncé, on doit obtenir:

$ ./a.out 
a-b--d
   --e---g----j
 -c--f---h
      ---i

Arbres $n$-aires

Cette partie est à faire en OCaml.

Un arbre $n$-aire est un arbre dont chaque nœud possède au plus $n$ fils, où $n$ est un entier naturel. Comme on ne travaille que sur des arbres finis, il existe un $n$ qui convient pour tout arbre.

On peut implémenter un tel arbre en utilisant un tableau ou une liste pour représenter les fils d’un nœud. Dans ce TP, on fait le choix d’implémenter l’arbre en représentation fils gauche / frère droit. La figure suivante illustre ce principe :

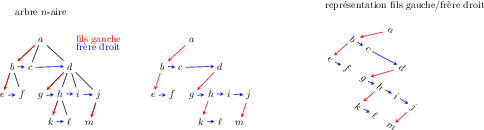
On définit les types suivants dans le fichier narbres.ml:

type narbre = NNoeud of int * narbre list

type arbre = Noeud of noeud
and noeud = { x : int; fg : arbre option; fd : arbre option}

Dans ce fichier sont également définis les arbres de l’exemple, sous les noms na et a.

On rappelle que pour exécuter du OCaml, on peut :

• utiliser utop et se servir de la méta-commande #use "toto.ml" pour inclure le code du fichier toto.ml (avec recommandation de sortir de utop à chaque fois qu’on modifie le contenu de toto.ml);
• compiler avec ocamlopt ou ocamlc : le code exécuté est la dernière définition du fichier source.

Exercice 7 : parcours préfixe

1. Écrire une fonction prefixe1 : narbre -> unit qui affiche les valeurs des nœuds d’un narbre, dans l’ordre du parcours préfixe.
2. Écrire une fonction prefixe2 : arbre option -> unit qui affiche les valeurs des nœuds d’un arbre, dans l’ordre du parcours préfixe, sans tenir compte que ça représente un arbre $n$-aire.
3. Tester sur na et a. Que remarquez-vous ? → à prouver dans le DM pour vendredi prochain

Exercice 8 : parcours postfixe et infixe

1. Écrire une fonction postfixe1 : narbre -> unit qui affiche les valeurs des nœuds d’un narbre, dans l’ordre du parcours postfixe.
2. Écrire une fonction infixe2 : arbre option -> unit qui affiche les valeurs des nœuds d’un arbre, dans l’ordre du parcours infixe, sans tenir compte que ça représente un arbre $n$-aire.
3. Tester sur na et a. Que remarquez-vous ? → à prouver dans le DM pour vendredi prochain

Exercice 9 : transformation

Écrire une fonction arbre_of_narbre : narbre -> arbre qui prend en argument un arbre $n$-aire et renvoie sa représentation fils gauche / frère droit.