TP7 : Compilation séparée et structures

Toutes les semaines, les TP sont à rendre pour le mercredi soir suivant au plus tard, sur cahier-de-prepa.

Chaque TP est composé de deux parties:

flocon : partie dédiée à ceux parmi vous qui n’ont jamais programmé ou se sentent en difficulté;
première étoile : partie dédiée à ceux qui sont à l’aise en programmation et à ceux qui ont réussi la partie flocon rapidement.

Le but de ceux qui choisissent la partie flocon doit être d’arriver petit à petit de plus en plus loin dans la partie première étoile.

Ceux qui choisissent la partie première étoile n’ont pas besoin de faire la partie flocon, et dans l’idéal doivent terminer la partie première étoile.

Pour ce TP, les réponses sont à rendre dans une archives contenant tous les fichiers (y compris ceux que je fournis), avec les noms spécifiés dans l’énoncé.

Plus sur la compilation

La compilation d’un programme C se fait en plusieurs étapes (et ces étapes peuvent dépendre du compilateur). Au moment où le compilateur passe dans un morceau de code où un identifiant (variable, fonction ou autre) est utilisé, il vérifie si les types qui apparaissent sont cohérents, par exemple pour une affectation si le type de la rvalue est compatible avec le type de la lvalue.

Le compilateur a donc, entre autres, besoin de connaître les types de retour des fonctions ainsi que les types de leurs paramètres. Si la fonction est définie (=en-tête+corps) avant son utilisation, il les connaît et peut procéder à des vérifications. Sinon ce n’est pas le cas, et la compilation produit une erreur.

Cette étape de vérification se fait lors de la compilation avant l’édition de liens qui est l’étape où le lien est effectivement fait entre un appel de fonction et la définition de cette fonction (c’est-à-dire son code).

Si une fonction g(...) appelle une fonction f(...) du même fichier, pour que le compilateur connaisse les types de f(...) avant cet appel, on peut par exemple définir f(...) avant g(...). Une autre méthode consiste à déclarer f(...) avant g(...) (en général avant de commencer à définir des fonctions), en écrivant sa signature (c’est-à-dire son en-tête) suivi d’un ;:

int f(int n);      // déclaration de f

void g(){
    int p = f(3);  // pas de problème car f a été déclarée avant
}

int f(int n){      // définition de f
    return n;
}

Fichiers d’en-tête

Quand on écrit un petit programme qui ne sera utilisé que par nous, cette solution de déclarer les fonctions en tête de fichier .c est parfaitement suffisante. Mais quand on écrit un programme dans le but qu’il soit réutilisé, elle est peu satisfaisante : on n’a pas forcément envie que l’utilisateur accède au code qu’on a écrit (ne serait-ce que parce qu’il peut le modifier par mégarde), mais on doit quand même lui fournir les en-têtes des fonctions et les définitions de types.

On a vu qu’il existe des fichiers d’en-tête (headers en anglais) qui permettent de déclarer des types et des fonctions. Ces fichiers portent l’extension .h. Un fichier d’en-tête ne sert pas à définir des fonctions, seulement à les déclarer (donc pas de corps de fonctions, que des en-têtes). Pour utiliser un fichier d’en-tête, il faut utiliser la directive de précompilation

#include <nom_du_fichier.h>

si le fichier d’en-tête se trouve dans les répertoires que gcc explorent par défaut, ou la directive

#include "nom_du_fichier.h"

s’il se trouve dans le même répertoire que le fichier source à compiler (on peu en fait mettre un chemin valide quelconque entre les guillemets).

On ne peut pas définir plusieurs fois la même entité en C, il est donc important qu’un fichier d’en-tête ne soit inclus qu’une seule fois. Pour ne pas avoir à gérer à la main des inclusions multiples, on utilise des macro-définitions: des valeurs pour le précompilateur qui lui permettent de savoir si le fichier a déjà été lu ou pas lors de la compilation (voir les fichiers d’en-tête fournis plus bas). Ainsi, tous vos fichiers d’en-tête doivent commencer par :

#ifndef _NOM_DU_FICHIER_H
#define _NOM_DU_FICHIER_H

et se terminer par :

#endif

Assez vite, on arrive à des fichiers sources trop longs, ou dont on voudrait pouvoir réutiliser une partie et pas l’autre par exemple. Pour structurer un programme, on peut bien entendu le séparer en plusieurs fichiers. Pour compiler un programme éparpillé sur plusieurs fichiers, il suffit de tous les donner en argument à gcc¹.

Flocon – pour ceux qui n’ont pas beaucoup programmé

Dans la partie flocon de ce TP, je vous fournis systématiquement:

pour les tests:
- un fichier d’en-tête avec des déclarations;
- un fichier source avec des tests : les corps des fonctions sont commentés, à vous de les décommenter au fur et à mesure de l’avancée de votre travail;
pour votre propre travail:
- un fichier d’en-tête qui contient uniquement les déclarations de types : vous devrez le compléter avec les macros qui évite une inclusion multiple et les signatures des fonctions que vous écrivez au fur et à mesure;
- un fichier dans lequel vous devez travailler, avec éventuellement quelques fonctions écrites (par exemple les fonctions liées aux fichiers).

Exercice 1 : Ensemble de Mandelbrot

Pour cet exercice, les fichiers de tests : tests_mandelbrot.h / tests_mandelbrot.c.

Et je vous fournis du code pour dessiner dans un fichier à partir d’un tableau bidimensionnel de booléens : dessin.h / dessin.c.

Vous ne devez ni écrire du nouveau code dans ces fichiers, ni copier le contenu de ces fichiers dans des nouveaux fichiers. (Vous pouvez juste décommenter du code dans le fichier de tests.)

Je vous fournis le fichier d’en-tête avec les définitions de types à utiliser : mandelbrot.h. À vous de le compléter et d’écrire un fichier mandelbrot.c contenant votre code.

On considère un point $C$ du plan de coordonnées $(x_c,y_c)$ et une suite de points $(P_n)_{n\geq 0}$ du plan. On note $(x_n, y_n)$ les coordonnées de $P_n$. Les coordonnées de $(P_n)_n$ sont obtenues par la relation de récurrence suivante :

\[\begin{array}{lcl} (x_0, y_0) &= & (0, 0)\\ (x_{n+1}, y_{n+1}) &=& (x_n^2-y_n^2+x_c, 2x_ny_n+y_c) \end{array}\]

L’ensemble de Mandelbrot est l’ensemble des points $C$ du plan pour lesquels la suite des points $(P_n)_n$ est bornée. On se propose d’obtenir une représentation graphique de cet ensemble.

Tous les points du plan seront considérés à coordonnées réelles (car $(1,1)$ n’est déjà plus dans l’ensemble de Mandelbrot). Il faudra donc mettre à la bonne échelle pour faire la représentation graphique.

Question 1. Écrire une fonction point_suivant qui possède 3 paramètres (dans cet ordre pour les tests):

1 paramètre pour un point de la suite
1 paramètres pour le point $C$
1 paramètres pour le point suivant dans la suite

et calcule les coordonnées du point suivant de la suite.

On donne la fonction norme_carre qui permet de calculer la norme au carré d’un point:

double norme_carree(struct point p){
  return p.x*p.x + p.y*p.y;
}

Question 2. En considérant que la suite des normes des $P_n$ est non bornée si au plus tard au bout de de 100 itérations, le point obtenu a atteint ou dépassé 2 en norme, écrire une fonction suite_bornee qui prend en argument le point $C$ et teste si la suite des normes est bornée.

Question 3. Écrire une fonction mandelbrot qui prend en argument deux entiers représentant la hauteur et la largeur d’une fenêtre et renvoyant un double pointeur sur booléen. Une case de ce tableau vaut true si et seulement si le point qu’elle représente est dans l’ensemble de Mandelbrot (attention à l’échelle : les points de l’ensemble de Mandelbrot ont des coordonnées de valeur absolue inférieure à 1). Je fournis une fonction sauvegarder qui permet de regarder le résultat visuel de votre fonction.

Avec les paramètre h=500 et l=500, j’obtiens l’image suivante:

Exercice 2 : Ensemble de Julia

Soit un point $C$ du plan, l’ensemble de Julia de $C$ est l’ensemble des points $(x_0, y_0)$ pour lesquels la suite $(P_n)_{n\geq 0}$ telle que définie à l’exercice précédent est bornée.

Écrire un programme permettant de donner en ligne de commande les valeurs de $x_C$ et $y_C$ (la fonction atof permet d’obtenir un double à partir d’une chaîne de caractères) et qui crée un fichier image contenant l’ensemble de Julia correspondant. (À vous d’écrire le fichier d’en-tête et le fichier de code séparement.)

Première étoile – pour ceux qui sont à l’aise en programmation et ceux qui ont facilement fini le flocon

Commencer par faire l’exercice 2 du niveau flocon.

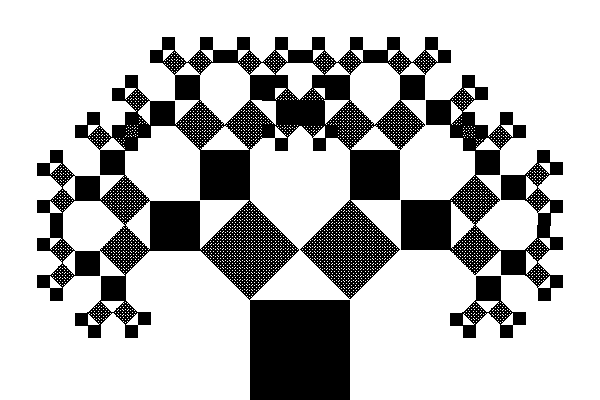
Exercice 3 : fractale de Pythagore

Le but de cet exercice est de dessiner la fractale appelée arbre de Pythagore :

Je vous fournis du code pour dessiner dans un fichier à partir d’un tableau bidimensionnel de booléens : dessin.h / dessin.c

et un fichier d’en-tête pour le code que vous devez écrire : pythagore.h.

Le principe de construction est de partir d’un carré et d’en construire deux autres de la manière suivante :

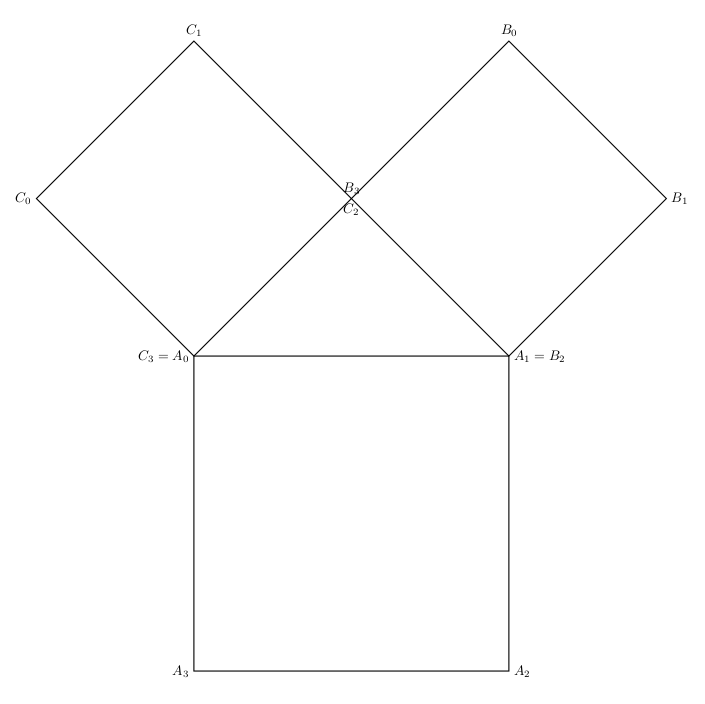
où on a pour les nouveaux sommets :

$C_0$ est l’image de $C_2$ par la rotation d’angle $\frac{\pi}{2}$ et de centre $A_0$,
$C_1$ est l’image de $A_0$ par la translation de vecteur $\overrightarrow{A_0C_0}+\overrightarrow{A_0C_2}$,
$C_2$ est l’image du milieu du segment $[A_0,A_1]$ par le vecteur $\frac{1}{2}\overrightarrow{A_2A_1}$,
$B_0$ est l’image de $A_1$ par la translation de vecteur $\overrightarrow{A_1B_3}+\overrightarrow{A_1B_1}$ et
$B_1$ est l’image de $B_3$ par la rotation d’angle $-\frac{\pi}{2}$ et de centre $A_1$.

Pour rappel, les coordonnées de l’image d’un point $(x, y)$ par une rotation de centre $(x_C, y_C)$ et d’angle $\theta$ sont $(x_c + (x-x_C)\cos\theta, y_C-(y-y_C)\sin\theta)$.

La documentation des fonctions demandées ci-dessous se trouve dans le fichier d’en-tête fourni.

Écrire le code des fonctions milieu, translate et vecteur.
Écrire le code de la fonction suivants.

On va maintenant fabriquer les carrés par génération.

Écrire le code de la fonction carre_initial.
Écrire le code de la fonction generation_suivante.

Il est temps de passer aux fonctions qui permettent de faire les dessins.

Écrire le code de la fonction fenetre : un pixel à false sera dessiné en blanc, un pixel à true en noir.
Pour dessiner le carré $(A_0A_1A_2A_3)$ dans une fenêtre, nous allons suivre l’algorithme suivant :
- on considère $\overrightarrow{u}$ (resp. $\overrightarrow{v}$) le vecteur unitaire de même direction et même sens que $\overrightarrow{A_0A_1}$ (resp. $\overrightarrow{A_0A_3}$),
- pour tout $\alpha$ (resp. $\beta$) entier de 0 à $||\overrightarrow{A_0A_1}||$ (resp. $||\overrightarrow{A_0A_3}||$), si le translaté de $A_0$ par le vecteur $\alpha \overrightarrow{u}+\beta \overrightarrow{v}$ est dans l’image, on met le pixel correspondant à true. Écrire le code de la fonction dessin.
Écrire le main qui permet d’obtenir 15 générations de carrés. Vous pouvez utiliser la fonction sauvegarder fournie pour obtenir un fichier au format png.

1: Dans la vrai vie, il existe des outils pour gérer la compilation des gros projets et notamment spécifier les dépendances entre tous les fichiers qui interviennent, ce qui évite de tout recompiler quand on ne modifie qu’un seul fichier par exemple, mais permet aussi de recompiler tout ce qu’il est nécessaire de recompiler sans se poser de questions à chaque fois. Ces outils sont hors programme, mais les plus curieux pourron jeter un œil à gnu make qui est sans doute l’outil de base le plus classique à cet effet pour le C.