TP5 : tableaux multidimensionnels statiques

Toutes les semaines, les TP sont à rendre pour le mercredi soir suivant au plus tard, sur cahier-de-prepa.

Les réponses sont à rendre dans un ou plusieurs fichiers sources, en ajoutant en commentaire vos nom et prénom sur la première ligne, la ligne de compilation à utiliser sur la deuxième ligne, et en identifiant de manière claire les numéros d’exercices et de questions.

Cette semaine, un seul énoncé qui est accompagné d’un code qu’il faut compléter.

Comme on n’a pas vu comment fournir un tableau en argument à une fonction, je vous donne les en-têtes de fonctions. Vous ne pouvez pas les comprendre, mais avec la documentation vous pouvez quand même utiliser les paramètres.

Le but de ce TP est d’écrire un programme qui permet de générer des pavages réguliers du plan. Un pavage du plan est une manière de couvrir le plan avec une infinité de copies du même polygone (ou d’un ensemble de polygones), de sorte que deux polygones ne se superposent pas et qu’il n’y ait pas de trous entre les polygones. Un pavage est dit régulier s’il y a moyen de le déplacer et de superposer le nouveau pavage obtenu avec le pavage d’origine (je ne prétends pas que c’est une définition mathématique).

exemples (que vous obtiendrez à la fin de ce TP) :

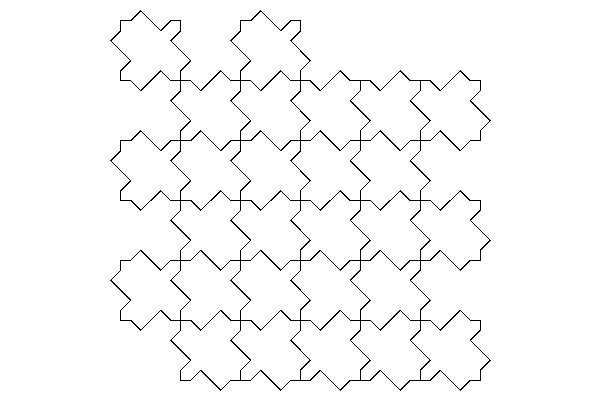
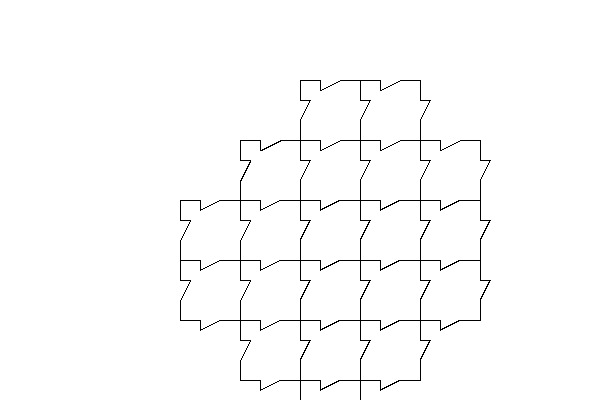
Un moyen de spécifier un pavage régulier, est de donner un polygone et un groupe d’isométries (oui, vous ne savez pas ce qu’est un groupe, disons pour simplifier un ensemble d’isométries et toutes les isométries qu’on peut obtenir en les composant autant de fois qu’on veut; et au cas où : une isométrie est une bijection du plan qui conserve les longueurs, vous en connaissez : translations, rotations, symétries) et d’appliquer ces isométries au polygone de départ.

Il se trouve qu’il y a exactement 17 groupes d’isométries qui permettent d’obtenir un pavage régulier. Si vous êtes curieux, vous pouvez regarder (après le TP) le site suivant : http://carmetal2.free.fr/articles/pavages.php.

La stratégie que nous allons adopter ici est de fabriquer un ensemble de composés des isométries de départ, puis de les appliquer un par un au polygone de départ.

Nous faisons les hypothèses suivantes:

• les points sont des pixels, on les représentera par un tableau de deux entiers,
• tous les polygones manipulés possèdent 20 sommets,
• nous cherchons à construire 50 isométries (y compris celles données au départ),
• la fenêtre d’affichage a pour dimension 600x400.

Je vous fournis un code pavage.c qui contient du code et des fonctions à compléter.

Appliquer les isométries

Exercice 1 :

Toute isométrie du plan peut être vue comme une matrice $3\times 3$ (pas n’importe quelle matrice, mais ce n’est pas le propos de cet énoncé). La composée de deux isométries est alors le produit de ces deux matrices.

Compléter le code de la fonction compose,

Exercice 2 :

L’image du point de coordonnées $(x,y)$ par une isométrie donnée par la matrice $M$ est obtenu en conservant les deux premières coordonnées du produit de $M$ et du vecteur

\begin{pmatrix}x\\y\\1\end{pmatrix}

Pour simplifier le propos, à partir de maintenant le point de coordonnées $(x, y)$ sera donc représenté par un tableau de trois entiers contenant dans l’ordre les entiers $x$, $y$ et $1$.

Compléter le code de la fonction bouge_point, puis celui de la fonction bouge_polygone.

Exercice 3 :

Comme mentionné plus haut, le but est d’appliquer un ensemble d’isométries à un polygone.

Compléter le code de la fonction dessin.

Fenêtre d’affichage

Notre affichage se faisant en noir et blanc (sans niveau de gris), nous allons représenter notre fenêtre d’affichage par un tableau bidimensionnel de taille 600x400 de booléens : un pixel vaudra alors vrai s’il doit être affiché en noir, et faux s’il doit être affiché en blanc.

Exercice 4 :

Le fond de l’image est donc blanc.

Compléter le code de la fonction initialise_fenetre.

Exercice 5 :

On a besoin de tracer des segments pour tracer un polygone. On adopte l’algorithme suivant pour tracer le segment $[PQ]$, où $P(x_P, y_P)$ et $Q(x_Q, y_Q)$ : on subdivise le segment $[PQ]$ en $\ell$ parties où $\ell$ est plus grand que sa longueur, et on trace les points $P+\frac{i}{\ell}\vec{PQ}$ pour $0\leq i<\ell$. Tracer un point signifie mettre le pixel correspondant à vrai.

(On peut décaler le pixel de $(300, 200)$ car la fenêtre graphique n’est pas centrée.)

Compléter le code de la fonction trace_segment.

Exercice 6 :

On peut maintenant tracer un polygone.

Compléter le code de la fonction trace_polygone.

Génération de l’ensemble des isométries

Il s’agit maintenant de suivre l’algorithme suivant :

• on a un ensemble $G_0$ d’isométries
• pour tout $n>0$, on fabrique l’ensemble $G_n$ des isométries obtenues en composant les isométries de $G_0$ et celles de $G_{n-1}$, sans dépasser 50 isométries.

Exercice 7 :

Compléter le code de la fonction generation.

Vous pouvez maintenant lancer votre programme !

Pour ceux qui ont fini et veulent aller plus loin

Exercice 8 :

Le traçage de segment de l’exercice 5 n’est pas très propre. Implémenter l’algorithme de Bresenham.

Exercice 9 :

Créer d’autres pavages vous aidant de http://carmetal2.free.fr/articles/pavages.php. (Ne pas oublier pas que nous avons fait l’hypothèse que les polygones ont 20 sommets.)